লম্ব বৃত্তাকার শঙ্কু কষে দেখি-16

NO:-1. । আমি একটি মুখবন্ধ লম্ব বৃত্তাকার শঙ্কু তৈরি করেছি যার ভূমির ব্যাসার্ধের দৈর্ঘ্য 15 সেমি. এবং তির্যক উচ্চতা 24 সেমি.। ওই শঙ্কুর পার্শ্বতিদের ক্ষেত্রফল ও সমগ্রতলের ক্ষেত্রফল হিসাব করে লিখি।

লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধের দৈর্ঘ্য 15 সেমি, তির্যক উচ্চতা 24 সেমি |

শঙ্কুর পার্শ্বতলের ক্ষেত্রফল এর সূত্র হল \(\pi rl\) বর্গ একক

\(1131\frac{3}{7}\)
পার্শ্বতলের ক্ষেত্রফল হল \(1131\frac{3}{7}\) বর্গ সেমি

লম্ব বৃত্তাকার শঙ্কুর ভূমির ক্ষেত্রফল নির্ণয় করার সূত্র হলো \(\pi r^{2}\) বর্গ একক |

\(\pi r^{2}\) বর্গ সেমি

\(\pi \times 15^{2}\) বর্গ সেমি

\(\frac{22}{7} \times 15^{2}\) বর্গ সেমি

\(\frac{22}{7} \times 15 \times 15\) বর্গ সেমি

\(\frac{4950}{7} \) বর্গ সেমি

\(4949\frac{1}{7} \) বর্গ সেমি

লম্ব বৃত্তাকার শঙ্কুর সমগ্র তলের ক্ষেত্রফলের সূত্র হল ভূমির ক্ষেত্রফল যুক্ত পার্শ্বতলের ক্ষেত্রফল |

ভূমির ক্ষেত্রফল + পার্শ্বতলের ক্ষেত্রফল =সমগ্র তলের ক্ষেত্রফলের
\(\pi r^{2}\)+\(\pi \times 15 \times 24\)=?
\(4949\frac{1}{7} \)+\(1131\frac{3}{7}\)

\(4949+\frac{1}{7} +1131+\frac{3}{7}\)

\(4949+1131+\frac{1}{7} +\frac{3}{7}\)

\(6080+\frac{1}{7} +\frac{3}{7}\)

\(6080+\frac{1+3}{7} \)

\(6080+\frac{4}{7} \)

\(6080\frac{4}{7} \)

অতএব পার্শতলের ক্ষেত্রফল হল \(1131\frac{3}{7}\) বর্গ সেমি, আর সমগ্র তলের ক্ষেত্রফল হলো \(6080\frac{4}{7} \) বর্গ সেমি |

NO.2:- শকুর আয়তন নির্ণয় করি যখন (1) ভূমির ক্ষেত্রফল 1.54 বর্গ মিটার এবং উচ্চতা 2.4 মিটার,

(i)এখানে ভূমির ক্ষেত্রফল হলো 1.54 বর্গমিটার | এখান থেকে আমরা লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ নির্ণয় করবো |
ধরিলাম লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ হলো r মিটার

শর্ত অনুযায়ী \(\pi r^{2}\)=1.54
\(\frac{22}{7}\times r^{2}=1.54\)
\(r^{2}=1.54\times \frac{7}{22}\)
\(r^{2}= \frac{154\times7}{100\times 22}\)
\(r^{2}= \frac{7\times7}{100\times 1}\)
\(r^{2}= \frac{7\times7}{100}\)
\(r^{2}= \frac{7\times7}{10\times 10}\)
\(r= \frac{7}{10}\)
\(r= 0.7\)

আয়তন নির্ণয় করার সূত্র \(\frac{1}{3}\times \pi \times r^{2} \times h\) ঘন একক | এখানে r ও h এর মান গুলি হল, r= 0.7 মিটার ও h=2.4 মিটার

\(\frac{1}{3}\times \pi \times 0.7^{2} \times 2.4\) ঘন মিটার

\(\frac{1}{3}\times \pi \times 0.7 \times 0.7 \times 2.4\) ঘন মিটার

\(\frac{1}{3}\times \frac{22}{7} \times 0.7 \times 0.7 \times 2.4\) ঘন মিটার

\(\frac{1}{3}\times \frac{22}{7} \times \frac{7}{10} \times \frac{7}{10} \times \frac{24}{10}\) ঘন মিটার

\(\frac{1}{3}\times \frac{22}{7} \times \frac{7}{10} \times \frac{7}{10} \times \frac{24}{10}\) ঘন মিটার

\(\frac{1}{3}\times \frac{22}{1} \times \frac{1}{10} \times \frac{7}{10} \times \frac{24}{10}\) ঘন মিটার

\(\frac{1}{1}\times \frac{22}{1} \times \frac{1}{10} \times \frac{7}{10} \times \frac{8}{10}\) ঘন মিটার

\(\frac{22 \times 7 \times 8}{1 \times 10 \times 10 \times 10 } \) ঘন মিটার

\(\frac{1232}{1 \times 10 \times 10 \times 10 } \) ঘন মিটার

\(\frac{1232}{1000 } \) ঘন মিটার

\(1.232 \) ঘন মিটার

NO.2:- শকুর আয়তন নির্ণয় করি যখন (ii) ভূমির ব্যাসের দৈর্ঘ্য 21 মিটার এবং তির্যক উচ্চতা 17.5 মিটার।

(ii) ভূমির ব্যাসের দৈর্ঘ্য 21 মিটার, ব্যাসাধের দৈর্ঘ্য \(\frac{21}{2}\) মিটার, ও তির্যক উচ্চতা 17.5 মিটার | এখানে প্রথমে উচ্চতা নির্ণয় করতে হবে |
ধরিলাম উচ্চতা হলো h মিটার |

সূত্র \(h^{2}+r^{2}=l^{2}\)

\(h^{2}+(\frac{21}{2})^{2}=17.5^{2}\)

\(h^{2}=17.5^{2}-(\frac{21}{2})^{2}\)

\(h^{2}=306.25-10.5^{2}\)

\(h^{2}=306.25-110.25\)

\(h^{2}=196\)

\(h=14\)

এই শঙ্কুটির আয়তন হবে \(\frac{1}{3}\times \pi \times 10.5^{2} \times 14\) ঘন মিটার (r=10.5, h=14)

\(\frac{1}{3}\times \frac{22}{7} \times 10.5^{2} \times 14\)

\(\frac{1}{3}\times \frac{22}{7} \times 10.5 \times 10.5\times 14\)

\(\frac{1}{3}\times \frac{22}{7} \times \frac{105}{10} \times \frac{105}{10} \times 14 \)

\(\frac{1}{1}\times \frac{22}{7} \times \frac{35}{10} \times \frac{105}{10} \times 14 \)

\(\frac{1}{1}\times \frac{22}{1} \times \frac{35}{10} \times \frac{105}{10} \times 2 \)

\(\frac{22}{1} \times \frac{35}{10} \times \frac{105}{10} \times 2 \)

\(\frac{22 \times 35 \times 105 \times 2}{1 \times 10 \times 10}\)

\(\frac{161700}{100}\)

1617

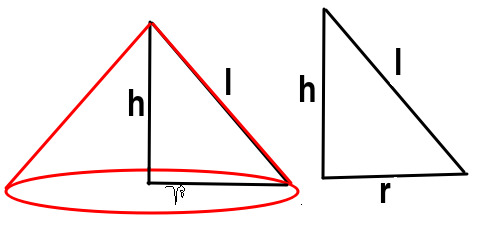
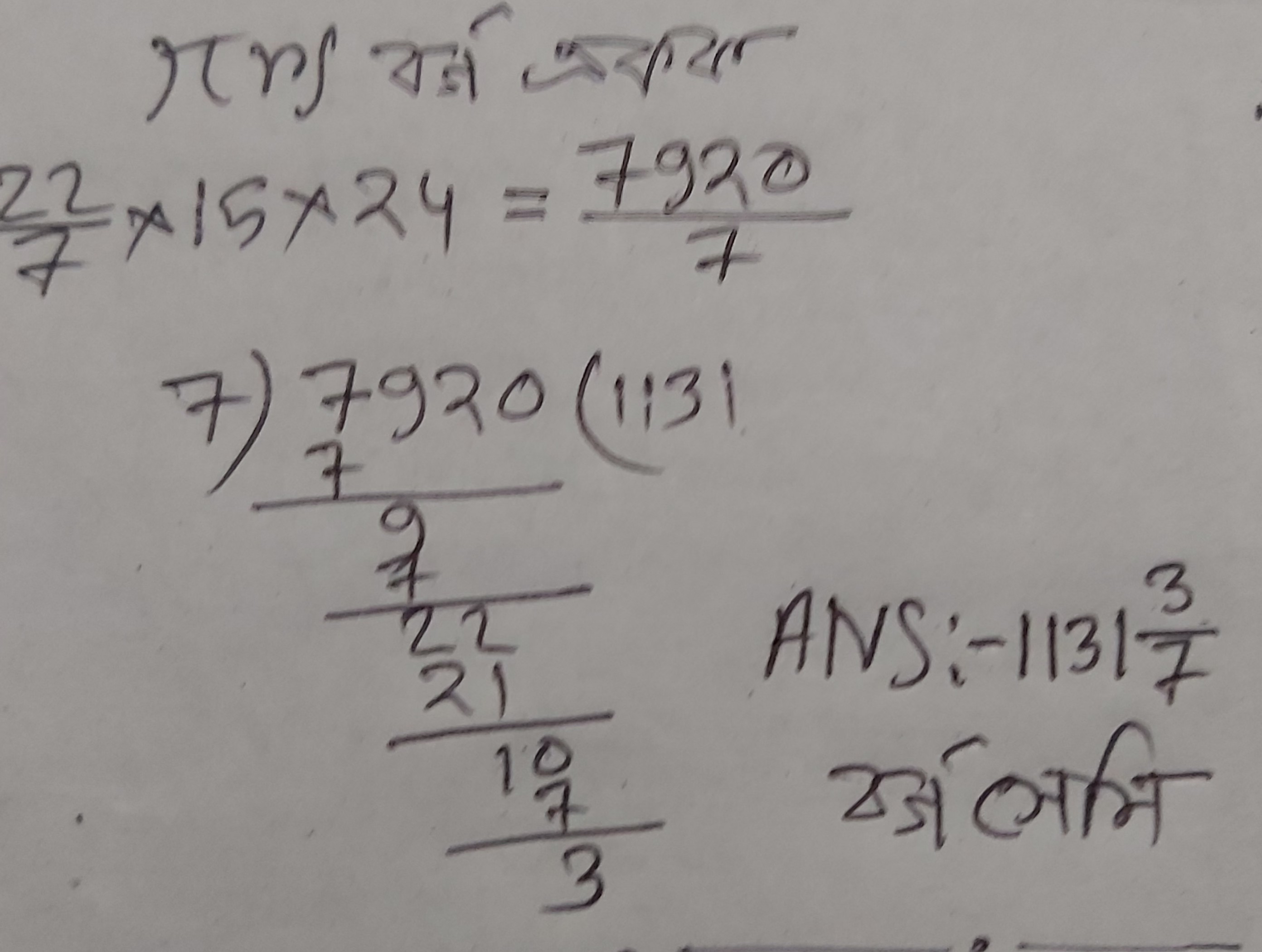NO.3:-আমিনা একটি সমকোণী ত্রিভুজ অঙ্কন করেছে যার সমকোণ সংলগ্ন বাহু দুটির দৈর্ঘ্য 15 সেমি. ও 20 সেমি। 15 সেমি. দীর্ঘ বাহুটিকে অক্ষ ধরে ত্রিভুজটিকে একবার পূর্ণ আবর্তন করলে যে ঘনবস্তু তৈরি হয়, তার পার্শ্বতলের ক্ষেত্রফল, সমগ্রতলের ক্ষেত্রফল এবং আয়তন নির্ণয় করি।

এখানে একটি সমকোণী ত্রিভুজ অঙ্কন করা হল | সমকোণ সংলগ্ন বাহু দুটির দৈর্ঘ্য 15 সেমি ও 20 সেমি | এখন 15 সেমি বাহু টিকে অক্ষ ধরে সমকোণী ত্রিভুজ টিকে একবার পূর্ণ আবর্তন করলে আমরা একটি লম্ব বৃত্তাকার শঙ্কু তৈরি করতে পারবো | এখন এই লম্ব বৃত্তাকার শঙ্কু টির ব্যাসার্ধ হবে 20 সেমি | কারন 20 সেমি দৈর্ঘ্যের বাহু টিকে পূর্ণ আবর্তন করানো হয়েছিল অর্থাৎ ঘোরানো হয়েছিল | আর 15 সেমি দৈর্ঘ্যের বাহু টি হল লম্ব বৃত্তাকার শঙ্কু উচ্চতা | কারণ এই বালুটি স্থির ছিল |

প্রথমে আমরা সমকোণী ত্রিভুজের অতিভুজ নির্ণয় করব | অতিভুজ নির্ণয় করার সূত্র হলো লম্ব\(^{2}\)+ ভূমি\(^{2}\)= অতিভুজ\(^{2}\) | এখানে লম্ব হল উচ্চতা অর্থাৎ 15 সেমি, ভূমি হল 20 সেমি, তির্যক উচ্চতা হল \(l\) সেমি |

ধরিলাম সমকোণী ত্রিভুজের অতিভুজ হলো \(l\) সেমি লম্ব\(^{2}\)+ ভূমি\(^{2}\)= অতিভুজ\(^{2}\)

\(15^{2}\)+ \(20^{2}\)=\(l^{2}\)

\(l^{2}=15^{2}+20^{2}\)

\(l^{2}=225+400\)

\(l^{2}=625\)

\(l=25\)

এখন নির্ণেয় তির্যক উচ্চতা হলো 25 সেমি

শঙ্কুর পার্শ্বতলের ক্ষেত্রফল নির্ণয় করার সূত্র \(\pi r l\) বর্গ একক

\(\pi \times 20 \times 25\)

\(\frac{22}{7} \times 20 \times 25\)

\(\frac{22 \times 20 \times 25}{7}\)

\(\frac{11000}{7}\)

\(1571\frac{3}{7}\) বর্গ সেমি

লম্ব বৃত্তাকার শঙ্কুর সমগ্রতলের ক্ষেত্রফল নির্ণয় করার অর্থ হলো ভূমির ক্ষেত্রফল যুক্ত পার্শতলের ক্ষেত্রফল যোগ করে যে ক্ষেত্রফল নির্ণয় হবে তাই হবে শঙ্কুটির সমগ্র তলের ক্ষেত্রফল | উপরে কিভাবে পার্শ্বতল নির্ণয় করা হয় তা জেনে নিয়েছি | এখন আমরা ভূমির ক্ষেত্রফল নির্ণয় করবো | ভূমির ক্ষেত্রফল মানে হলো একটি বৃত্তের ক্ষেত্রফল, কারন লম্ব বৃত্তাকার শঙ্কুর ভূমি হলো একটি বৃত্ত |

ভূমির ক্ষেত্রফল নির্ণয় করার সূত্র হল \(\pi r^{2}\) বর্গ একক

\(\pi \times 20^{2}\)

\(\frac{22}{7} \times 20 \times 20\)

\(\frac{22 \times 400}{7}\)

\(\frac{8800}{7}\)

\(1257\frac{1}{7}\) বর্গ সেমি

এখন লম্ব বৃত্তাকার শঙ্কুর ভূমির ক্ষেত্রফল হলো \(1257\frac{1}{7}\) বর্গ সেমি

সমগ্র তালের ক্ষেত্রফল এর সূত্র (পার্শ্বতলের ক্ষেত্রফল+ভূমির ক্ষেত্রফল=সমগ্র তালের ক্ষেত্রফল)
\(1571\frac{3}{7}\)+\(1257\frac{1}{7}\)

\(1571+1257+\frac{1}{7}+\frac{3}{7}\)

\(2828+\frac{1+3}{7}\)

\(2828+\frac{4}{7}\)

\(2828\frac{4}{7}\) বর্গ সেমি

নির্ণেয় সমগ্রতলের ক্ষেত্রফল হলো \(2828\frac{4}{7}\) বর্গ সেমি

লম্ব বৃত্তাকার শঙ্কুর আয়তন নির্ণয় করার সূত্র হলো \(\frac{1}{3} \pi r^{2} h\) ঘন একক |

\(\frac{1}{3} \pi \times 20^{2} \times 15\) ঘন সেমি

\(\frac{1}{3} \times \frac{22}{7} \times 20^{2} \times 15\) ঘন সেমি

\(\frac{1}{3} \times \frac{22}{7} \times 20 \times 20 \times 15\) ঘন সেমি

\(\frac{1 \times 22 \times 20 \times 20 \times 15}{3 \times 7} \) ঘন সেমি

\(\frac{132000}{21} \) ঘন সেমি

\(6285\frac{15}{21} \) ঘন সেমি

\(6285\frac{5}{7} \) ঘন সেমি

নির্ণেয় আয়তন হলো \(6285\frac{5}{7} \) ঘন সেমি

অতএব লম্ব বৃত্তাকার শঙ্কুটির পার্শ্বতলের ক্ষেত্রফল হল \(1571\frac{3}{7}\) বর্গ সেমি, সমগ্রতলের ক্ষেত্রফল হলো \(2828\frac{4}{7}\) বর্গ সেমি, আয়তন হলো \(6285\frac{5}{7} \) ঘন সেমি |

NO.4:-কোনো শত্রুর উচ্চতা ও তির্যক উচ্চতা যথাক্রমে 6 সেমি. ও 10 সেমি. হলে, শঙ্কুটির সমগ্রতলের ক্ষেত্রফল ও আয়তন নির্ণয় করি।

এই লম্ব বৃত্তাকার শঙ্কু অঙ্কটিতে উচ্চতা ও তির্যক উচ্চতা দেওয়া আছে | উচ্চতা হল 6 সেমি ও তির্যক উচ্চতা হল 10 সেমি | এখান থেকে আমাকে প্রথমে ব্যাসার্ধ নির্ণয় করতে হবে |

ধরিলাম শঙ্কুটির ব্যাসার্ধ হল r সেমি |
\(h^{2}+r^{2}=l^{2}\)

\(6^{2}+r^{2}=10^{2}\)

\(r^{2}=10^{2}-6^{2}\)

\(r^{2}=100-36\)

\(r^{2}=64\)

\(r=8\) সেমি

শঙ্কুটির আয়তন হবে \(frac{1}{3} \pi r^{2}h\) ঘন একক

\(\frac{1}{3} \pi \times 8^{2} \times 6\) ঘন সেমি

\(\frac{1}{3} \times \pi \times 64 \times 6\)

\(\frac{1}{1} \times 64 \times 2 \times \pi\)

\(64 \times 2 \times \pi\)

\(64 \times 2 \times \pi \)

\(128 \frac{22}{7}\) ঘন সেমি

\(\frac{22\times 128}{7}\) ঘন সেমি

\(\frac{2816}{7}\) ঘন সেমি

\(402\frac{2}{7}\) ঘন সেমি

NO.5:-কোনো লম্ব বৃত্তাকার শঙ্কুর আয়তন \(100\pi\) ঘন সেমি. এবং উচ্চতা 12 সেমি. হলে, শঙ্কুর তির্যক উচ্চতা হিসাব করে লিখি।

5 এখানে লম্ব বৃত্তাকার শঙ্কুর আয়তন \(100\pi\) ঘন সেমি | উচ্চতা 12 সেমি | আমাদের কে তির্যক উচ্চতা নির্ণয় করতে হবে | আমরা শঙ্কুর আয়তন নির্ণয় করার সূত্র জানি | সূত্রটি হলো \(\frac{1}{3}\pi r^{2} h\) | h=উচ্চতা, r=ব্যাসার্ধ |

এখন শর্ত অনুযায়ী \(\frac{1}{3}\pi r^{2} h\)=\(100\pi\)

\(\frac{1}{3}\pi r^{2} h=100\pi\)

\(\frac{1}{3} r^{2} h=100\)

\(r^{2} h=100\times \frac{3}{1} \)

\(r^{2} h=100\times 3 \)

\(r^{2} h=300 \)

\(r^{2}\times 12=300 \) h এর মান 12 বসিয়ে পাই

\(r^{2}\times=\frac{300}{12} \)

\(r^{2}\times=\frac{150}{6} \)

\(r^{2}\times=\frac{50}{2} \)

\(r^{2}\times=25 \)

তির্যক উচ্চতা নির্ণয় করার সূত্র হল সমকোণী ত্রিভুজের অতিভুজ নির্ণয় করার সূত্র, অর্থাৎ লম্ব\(^{2}\)+ ভূমি\(^{2}\)= অতিভুজ\(^{2}\) | এখানে লম্ব মানে লম্ব বৃত্তাকার শঙ্কুর উচ্চতা অর্থাৎ h, ভূমি মানে লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ অর্থাৎ r| ধরিলাম লম্ব বৃত্তাকার শঙ্কুর তির্যক উচ্চতা \(l\) | \(h^{2}+r^{2}=l^{2}\) এই সূত্র ব্যবহার করে লম্ব বৃত্তাকার শঙ্কুর এর তির্যক উচ্চতা নির্ণয় নির্ণয় করা যাবে |

\(12^{2}+25=l^{2}\)

\(l^{2}=12^{2}+25\)

\(l^{2}=144+25\)

\(l^{2}=169\)

\(l=13\)

অতএব লম্ব বৃত্তাকার শঙ্কুর তির্যক উচ্চতা হল 13 সেমি |

NO.6:-লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবু তৈরি করতে 77 বর্গ মিটার ত্রিপল লেগেছে। তাঁবুটির তির্যক উচ্চতা যদি 7 মিটার হয়, তবে তাঁবুটির ভূমিতলের ক্ষেত্রফল হিসাব করে লিখি।

6 এখানে লম্ব বৃত্তাকার শঙ্কু আকৃতির তাঁবু তৈরি করতে 77 বর্গ মিটার ত্রিপল ব্যবহার করা হয়েছে | অর্থাৎ লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল 77 বর্গমিটার | কারণ ভূমিতে কোনো ত্রিপল ব্যবহার করা হয় নি বলে ধরে নিলাম |

লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের বা বক্রতল ক্ষেত্রফল এর সূত্র \(\pi rl\) বর্গ একক
শর্ত অনুযায়ী \(\pi rl\)=77

\(\pi \times r \times 7\)=77 \(l\) এর মান 7 বসিয়ে পাই

\(\frac{22}{7} \times r \times 7=77\)

\(\frac{22}{7} \times r \times 7=77\)

\(r \times 7=77\times \frac{7}{22} \)

\(r=77\times \frac{7}{22 \times 7} \)

\(r=11\times \frac{7}{22} \)

\(r=1\times \frac{7}{2} \)

\(r=\frac{7}{2} \)

লম্ব বৃত্তাকার শঙ্কু আকৃতি তাঁবুটির ভূমির ক্ষেত্রফল মানে একটি বৃত্তের ক্ষেত্রফল নির্ণয় করার সূত্র, অর্থাৎ সূত্রটি হলো \(\pi r^{2}h\) বর্গ একক

\(\pi r^{2}\)

\(\pi \times (\frac{7}{2})^{2}\) r এর মান \(\frac{7}{2} \) বসিয়ে পাই

\(\frac{22}{7}\times (\frac{7}{2})^{2}\)

\(\frac{22}{7}\times \frac{7}{2} \times \frac{7}{2}\)

\(\frac{11}{7}\times \frac{7}{1} \times \frac{7}{2}\)

\(\frac{11}{1}\times \frac{1}{1} \times \frac{7}{2}\)

\(11 \times \frac{7}{2}\)

\(11 \times 3.5\)

\(38.5\)

অতএব লম্ব বৃত্তাকার শঙ্কু আকৃতির তাঁবু টির ভূমির ক্ষেত্রফল হবে 38.50 বর্গ মিটার |

NO.7:-একটি লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাস 21 মিটার এবং উচ্চতা 14 মিটার। প্রতি বর্গ মিটার 1.50 টাকা হিসাবে পার্শ্বতল রং করতে কত টাকা খরচ পড়বে হিসাব করি।

7 লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাস 21 মিটার, ব্যাসার্ধ r=\(\frac{21}{2}\) মিটার, উচ্চতা h=14 মিটার, এখানে তির্যক উচ্চতা \(l\) নির্ণয় করতে হবে | সূত্র লম্ব\(^{2}\)+ ভূমি\(^{2}\)= অতিভুজ\(^{2}\) | \(h^{2}+r^{2}=l^{2}\)

\(l^{2}=h^{2}+r^{2}\)

\(l^{2}=14^{2}+(\frac{21}{2})^{2}\)

\(l^{2}=14^{2}+10.5^{2}\)

\(l^{2}=196+110.25\)

\(l^{2}=306.25\)

\(l=17.5\)

এখন পার্শ্বতলের ক্ষেত্রফল নির্ণয় করতে হবে | শঙ্কুর পার্শ্বতল ক্ষেত্রফল নির্ণয় করার সূত্র হল \(\pi rl\) বর্গ একক

\(\pi rl\)

\(\pi \times \frac{21}{2} \times 17.5\) r ও \(l\) এর মান \(\frac{7}{2} \), 17.5 বসিয়ে পাই

\(\frac{22}{7} \times \frac{21}{2} \times 17.5\)

\(\frac{11}{7} \times \frac{21}{1} \times 17.5\)

\(\frac{11}{1} \times \frac{3}{1} \times 17.5\)

\(11 \times 3 \times 17.5\)

\(577.5\)

পার্শ্বতলের ক্ষেত্রফল 577.5 বর্গমিটার

1 বর্গ মিটারে খরচ হয় 1.50 টাকা
577.5 বর্গ মিটারে খরচ হয় \(577.5\times 1.50\) টাকা
\(577.5\times 1.50\)=866.25 টাকা

অতএব লম্ব বৃত্তাকার শঙ্কু টির পার্শ্ব তল রং করতে মোট 866.25 টাকা খরচ হবে

NO.8:-শঙ্কু আকৃতির একটি কাঠের খেলনার ভূমিতলের ব্যাসের দৈর্ঘ্য 10 সেমি.। খেলনাটির চারপাশ প্রতি বর্গ সেমি. 2.10 টাকা হিসাবে পালিশ করতে 429 টাকা খরচ পড়ে। খেলনাটির উচ্চতা কত হিসাব করি। খেলনাটি তৈরি করতে কত ঘন সেমি. কাঠ লেগেছে নির্ণয় করি।

8 প্রথমে কাঠের খেলনার পার্শতলের ক্ষেত্রফল নির্ণয় করতে হবে |

2.10 টাকায় পালিশ করা যায় 1 বর্গ সেমি
1 টাকায় পালিশ করা যায় \(\frac{1}{2.10}\) বর্গ সেমি
429 টাকায় পালিশ করা যায় \(\frac{1 \times 429}{2.10}\) বর্গ সেমি
\(\frac{1 \times 429}{2.10}\)=\(\frac{429}{2.10}\) বর্গ সেমি

এখন কাঠের খেলনার পার্শতলের অর্থাৎ বক্রতলের ক্ষেত্রফল পেলাম \(\frac{429}{2.10}\) বর্গ সেমি | এরপর আমরা লম্ব বৃত্তাকার শঙ্কুটির তির্যক উচ্চতা নির্ণয় করতে পারবে | শঙ্কুর তির্যক উচ্চতা নির্ণয় করার সূত্র হলো \(\pi r l\) বর্গ একক | এখানে \(\pi r l\)= \(\frac{429}{2.10}\) বর্গ সেমি হবে | এর পর সমাধান করিলে \(l\) এর মান পাবো |

\(\pi r l=\frac{429}{2.10}\)

\(\frac{22}{7} \times r \times l=\frac{429}{2.10}\)

\(\frac{22}{7} \times 5 \times l=\frac{429}{2.10}\) r এর মান 5 বসিয়ে পাই

\(5 \times l=\frac{429}{2.10} \times \frac{7}{22}\)

\(l=\frac{429}{2.10} \times \frac{7}{22 \times 5}\)

\(l=\frac{429 \times 7}{2.10 \times 22 \times 5} \)

\(l=\frac{429}{0.30\times 22 \times 5} \)

\(l=\frac{19.5}{0.30 \times 5} \)

\(l=\frac{3.9}{0.30} \)

\(l=13\)

অর্থাৎ লম্ব বৃত্তাকার শঙ্কুটির তির্যক উচ্চতা হলো 13 সেমি

ধরিলাম খেলনাটির উচ্চতা h সেমি
\(h^{2}+5^{2}=13^{2}\)
\(h^{2}+25=169\)
\(h^{2}=169-25\)
\(h^{2}=144\)
\(h=12\)
নির্ণেয় উচ্চতা হলো 12 সেমি

এরপর লম্ব বৃত্তাকার শঙ্কু এর আয়তন নির্ণয় করবো | আয়তন নির্ণয় করার সূত্র হলো \(\frac{1}{3}\pi r^{2}h\) | আমি উপরে h এর মান নির্ণয় করেছি | h এর মান হলো 12 সেমি | সূত্রে r ও h এর মান বসালে লম্ব বৃত্তাকার শঙ্কু এর আয়তন কত তা জানতে পারা যাবে |

সূত্র \(\frac{1}{3}\pi r^{2}h\)

মান বসানোর পর \(\frac{1}{3}\times \pi \times 5^{2}\times 12\)

\(\frac{1}{3}\times \frac{22}{7} \times 5^{2}\times 12\)

\(\frac{1}{3}\times \frac{22}{7} \times 25 \times 12\)

\(\frac{1}{1}\times \frac{22}{7} \times 25 \times 4\)

\(\frac{22}{7} \times 25 \times 4\)

\(\frac{22 \times 25 \times 4 }{7}\)

\(\frac{2200}{7}\)

\(314\frac{2}{7}\)

\(314.285714286\)

অতএব শঙ্কু আকৃতির খেলনাটির আয়তন হলো \(314\frac{2}{7}\) ঘন সেমি | এটিকে দশমিক আকারে করলে হবে 314.285714286 ঘন সেমি = 314.29 ঘন সেমি |

NO.9:-লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি লোহার পাতের বয়া তৈরি করতে \(75\frac{3}{7}\) বর্গ মিটার লোহার পাত লেগেছে। বয়াটির তির্যক উচ্চতা যদি 5 মিটার হয়, তবে বয়াটিতে কত বায়ু আছে এবং বয়াটির উচ্চতা কত হিসাব করে লিখি। ওই বয়াটির চারপাশ রং করতে প্রতি বর্গ মিটার 2.80 টাকা হিসাবে কত খরচ পড়বে নির্ণয় করি। [লোহার পাতের বেধ হিসাবের মধ্যে ধরতে হবে না]

9 এখানে লম্ব বৃত্তাকার শঙ্কু আকৃতির বয়া তৈরি হয়েছে লোহার পাত দিয়ে | বয়াটির মাঝের অংশ ফাঁপা | বয়াটির দুটি তল আছে, তল দুটি তে লোহার পাত ব্যবহার করা হয়েছে | তল দুটি তৈরি করতে মোট \(75\frac{3}{7}\) বর্গ মিটার লোহার পাত এর ব্যবহার হয়েছে | অর্থাৎ বয়াটির পার্শ্বতল ও ভূমি তৈরি করতে মোট \(75\frac{3}{7}\) বর্গ মিটার লোহার পাত এর প্রয়োজন হয়েছিল |

\((\pi r^{2})\)+\((\pi r l )\)

শর্ত অনুযায়ী \((\pi r^{2})\)+\((\pi r l )\)=\(75\frac{3}{7}\)

\((\pi \times r^{2})+(\pi \times r \times 5 )=75\frac{3}{7}\) (\(l\)=5)

\(\pi (r^{2} +5r)=75\frac{3}{7}\)

\(\frac{22}{7} (r^{2} +5r)=75\frac{3}{7}\)

\((r^{2} +5r)=75\frac{3}{7} \times \frac{7}{22} \)

\((r^{2} +5r)=\frac{528}{7} \times \frac{7}{22} \)

\((r^{2} +5r)=\frac{528}{1} \times \frac{1}{22} \)

\((r^{2} +5r)=\frac{24}{1} \times \frac{1}{1} \)

\((r^{2} +5r)=24 \)

\(r^{2} +5r-24=0 \)

\(r^{2} +8r-3r-24=0 \)

\(r(r+8)-3(r+8)=0 \)

\((r-3)(r+8)=0 \)

ধরিলাম বয়াটির উচ্চতা h মিটার
উচ্চতা নির্ণয় করার সূত্র \(h^{2}+r^{2}=l^{2} \)
\(h^{2}+3^{2}=5^{2} \) (r=3,l=5)
\(h^{2}+9=25\)
\(h^{2}=25-9\)
\(h^{2}=16\)
\(h=4\)
অতএব বয়াটির উচ্চতা হল 4 মিটার

এরপর নির্ণয় করিবো লম্ব বৃত্তাকার শঙ্কু আকৃতির বয়াটির মধ্যে কত পরিমান বায়ু আছে | অর্থাৎ বায়ুর আয়তন কত পরিমাণ | আয়তন নির্ণয় করার সূত্র এর মাধ্যমে বায়ুর আয়তন নির্ণয় করব |

আয়তন নির্ণয় করার সূত্র \(frac{1}{3} \pi r^{2} h\)

\(\frac{1}{3} \times \pi \times 3^{2} \times 4\) (r=3, h=4)

\(\frac{1}{3} \times \frac{22}{7} \times 3^{2} \times 4\)

\(\frac{1}{3} \times \frac{22}{7} \times 9 \times 4\)

\(\frac{1}{1} \times \frac{22}{7} \times 3 \times 4\)

\(\frac{22 \times 3 \times 4 }{7}\)

\(\frac{264}{7}\)

\(37\frac{5}{7}\)

অতএব বয়াটির মধ্যে বায়ুর আয়তন এর পরিমাণ হলো \(37\frac{5}{7}\) ঘন মিটার

NO.10:-লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবুতে 11জন লোক থাকতে পারে। প্রত্যেক লোকের জন্য ভূমিতে 4 বর্গ মিটার জায়গা লাগে এবং 20 ঘন মিটার বাতাসের প্রয়োজন। ঠিক এই 11 জন লোকের জন্য নির্মিত তাঁবুর উচ্চতা নির্ণয় করি।

দশম শ্রেণীর গণিত প্রকাশ অংক বইয়ের লম্ব বৃত্তাকার শঙ্কু অর্থাৎ কষে দেখি 16 চেপ্টাটির 10 নম্বর দাগের অঙ্কটিতে তাবুর মধ্যে বাতাসের আয়তন 20 ঘন মিটার আছে | তাবুর মধ্যে বাতাসের আয়তন যদি 220 ঘন মিটার হয় তাহলে অঙ্ক বই এর উত্তর অনুযায়ি তাবুর উচ্চতা 15 মিটার হবে | 20 ঘনমিটার নিয়ে সমাধান করিলে তাঁবুর উচ্চতা হবে | আমি 220 ঘন মিটার নিয়ে সমাধান করিলাম |

একটি তাবুর মধ্যে 11 জন লোক থাকে | লোক গুলি থাকার জন্য তাবুর ভূমিতে জায়গার প্রয়োজন হয় | অঙ্কে বলা আছে একটি লোকের জন্য 4 বর্গমিটার জায়গা লাগে | তাহলে 11 জন লোক এর জন্য \(4 \times 11= 44\) বর্গমিটার জায়গা লাগবে | এখন এই 44 বর্গমিটার জায়গা হলো লম্ব বৃত্তাকার শঙ্কু আকৃতির তাবুটির ভূমির ক্ষেত্রফল | এখন আমরা প্রথমে ভূমির ব্যাসার্ধ নির্ণয় করিব |

1 জনের জন্য জায়গা লাগে 4 বর্গমিটার
11 জনের জন্য জায়গা লাগে \(4 \times 11= 44\) বর্গমিটার

শর্ত অনুযায়ী ভূমির ক্ষেত্রফল \(\pi r^{2}= 44\) বর্গমিটার

220 ঘন মিটার বাতাস লম্ব বৃত্তাকার শঙ্কু আকৃতির তাঁবুটির মধ্যে আছে | তাই তাঁবুটির আয়তন হল 220 ঘন মিটার |

শর্ত অনুযায়ী \(\frac{1}{3} \pi r^{2} h=220\)

\(\frac{1}{3} \times \pi r^{2} \times h=220\)

\(\pi r^{2}\) এর মান একত্রে হলো 44
\(\frac{1}{3} \times 44 \times h=220\)

\(h=220 \times \frac{3}{1 \times 44}\)

\(h=5 \times \frac{3}{1 \times 1}\)

\(h=5 \times 3\)

\(h=15\)

অতএব তাঁবুটির নির্ণেয় উচ্চতা হলো 15 মিটার

NO.11:-শোলা দিয়ে তৈরি একটি শঙ্কু আকৃতির মাথার টোপরের ভূমির বাইরের দিকের ব্যাসের দৈর্ঘ্য 21 সেমি.। টোপরটির উপরিভাগ রাংতা দিয়ে মুড়তে প্রতি বর্গ সেমি. 10 পয়সা হিসাবে 57.75 টাকা খরচ পড়ে। টোপরটির উচ্চতা ও তির্যক উচ্চতা হিসাব করে লিখি।

10 পয়সা মানে হলো 0.10 টাকা| শঙ্কু আকৃতির টোপরের পার্শ্বতল অর্থাৎ বক্রতল এর ক্ষেত্রফল নির্ণয় করতে হবে |

0.10 টাকায় রাংতা দিয়ে মুড়তে পারা যায় 1 বর্গসেমি |
1 টাকায় রাংতা দিয়ে মুড়তে পারা যায় \frac{1}{0.10} বর্গসেমি |
57.75 টাকায় রাংতা দিয়ে মুড়তে পারা যায় \frac{1\times 57.75}{0.10} বর্গসেমি |
\frac{1\times 57.75}{0.10}

\frac{57.75}{0.10}

\frac{5775\times 100}{10\times 100}

\frac{5775}{10}

577.5 বর্গসেমি

এখন শঙ্কুটির বক্রতলের ক্ষেত্রফল পেলাম 577.5 বর্গসেমি |

ধরিলাম শঙ্কু আকৃতির টোপরের উচ্চতা হলো h সেমি, আর তির্যক উচ্চতা হলো \(l \) সেমি | ব্যাস এর দৈর্ঘ্য দেওয়া আছে 21 সেমি, তাহলে ব্যাসার্ধ এর দৈর্ঘ্য হবে \(\frac{21}{2} \) সেমি | প্রথমে আমি তির্যক উচ্চতা নির্ণয় করব, শঙ্কুর পার্শ্বতলের ক্ষেত্রফল নির্ণয় করার সূত্র ব্যবহার করে | সূত্র টি হলো \(\pi r l \) বর্গসেমি

শর্ত অনুযায়ী \(\pi r l =577.5\)

\(\frac{22}{7} \times r \times l =577.5\)

\(\frac{22}{7} \times \frac{21}{2} \times l =577.5\) (r এর মান বসিয়ে পাই r= \(\frac{21}{2} \))

\(\frac{11}{7} \times \frac{21}{1} \times l =577.5\)

\(\frac{11\times 21}{7} \times l =577.5\)

\(l =52.5 \times \frac{7}{1 \times 21}\)

\(l =2.5 \times \frac{7}{1 \times 1}\)

\(l =2.5 \times 7\)

\(l =17.5\)

শঙ্কু আকৃতি টোপরের তির্যক উচ্চতা হলো 17.50 সেমি |

শঙ্কু আকৃতির টোপরের উচ্চতা নির্ণয় করবো সমকোণী ত্রিভুজের লম্ব\(^{2}\)+ ভূমি\(^{2}\)= অতিভুজ\(^{2}\) সূত্র ব্যবহার করে | যেখানে লম্ব=h, ভূমি=r, অতিভুজ= \( l \)

\(h^{2}+(\frac{21}{2})^{2}=17.50^{2}\)

\(h^{2}+10.50^{2}=17.50^{2}\)

\(h^{2}=17.50^{2}-10.50^{2}\)

\(h^{2}=306.25-110.25\)

\(h^{2}=196\)

\(h=14\)

অতএব উচ্চতা হলো 14 সেমি

NO.12:-গমের একটি স্তূপ লম্ব বৃত্তাকার শঙ্কু আকারে আছে, যার ভূমির ব্যাসের দৈর্ঘ্য 9 মিটার এবং উচ্চতা 3.5 মিটার। মোট গমের আয়তন নির্ণয় করি। গমের ওই স্তূপ ঢাকতে কমপক্ষে কত বর্গ মিটার প্লাসটিকের চাদর প্রয়োজন হবে হিসাব করে দেখি। [ধরি, \(\pi\)= 3.14,\(\sqrt{130}\)= 11.4]

12 গমের স্তূপের আয়তন হলো \(\frac{1}{3} \pi r^{2}h\)

\(\frac{1}{3}\pi \times ((\frac{9}{2})^{2} \times 3.5\) যেখানে r= \(\frac{9}{2}\), h=3.5

\(\frac{1}{3}\times 3.14 \times (\frac{9}{2})^{2} \times 3.5\) কারণ \(\pi=3.14\)

\(\frac{1}{3}\times 3.14 \times \frac{9}{2} \times \frac{9}{2} \times 3.5\)

\(\frac{1}{1}\times 3.14 \times \frac{3}{2} \times \frac{9}{2} \times 3.5\)

\(3.14 \times \frac{3}{2} \times \frac{9}{2} \times 3.5\)

\(1.57 \times \frac{3}{1} \times \frac{9}{2} \times 3.5\)

\(1.57 \times 3 \times \frac{9}{1} \times 1.75\)

\(1.57 \times 3 \times 9 \times 1.75\)

74.1825=74.18

অতএব শঙ্কু আকৃতির স্তুপটিতে গমের আয়তন হল 74.18 ঘন মিটার |

লম্ব বৃত্তাকার শঙ্কু আকৃতির গমের স্তুপ টিকে প্লাস্টিকের চাদর দিয়ে ঢাকা হবে | অর্থাৎ প্লাস্টিকের চাদরটি হলো গমের স্তূপ এর পার্স তল | অঙ্কটি থেকে আমরা স্তুপ টির উচ্চতা ও ব্যাসার্ধ জানতে পারি | উচ্চতা=3.5 মিটার, ব্যাসার্ধ=\(\frac{9}{2}\) মিটার | আমাকে গমের স্তুপ টির তির্যক উচ্চতা নির্ণয় করতে হবে | তির্যক উচ্চতা পেয়ে গেলে শঙ্কুটির পার্শ্বতলের ক্ষেত্রফল জানতে পারবো |

ধরিলাম গমের স্তুপ টির তির্যক উচ্চতা \(l\) মিটার

সূত্র লম্ব\(^{2}\)+ ভূমি\(^{2}\)= অতিভুজ\(^{2}\) | \(h^{2}+r^{2}=l^{2}\)

\(3.5^{2}+(\frac{9}{2})^{2}=l^{2}\), (\(r=\frac{9}{2}\), h=3.5)

\(3.5^{2}+(\frac{9}{2})^{2}=l^{2}\)

\(l^{2}=3.5^{2}+(\frac{9}{2})^{2}\)

\(l^{2}=3.5^{2}+4.5^{2}\)

\(l^{2}=12.25+20.25\)

\(l^{2}=32.5\)

এখান থেকে আমরা \(l\) এর মান পেলাম \(\sqrt{32.5}\) মিটার | এর পর ত্রিপল এর ক্ষেত্রফল নির্ণয় করবো | সূত্রটি হলো \(\pi r l\) বর্গ একক |

\(3.14 \times \frac{9}{2} \times \sqrt{32.5} \)

\(3.14 \times \frac{9}{2} \times 5.700877125 \)

\(3.14 \times 4.5 \times 5.70 \)

\(80.541 \) =80.54

অতএব গমের স্তূপ টিকে ঢাকতে ত্রিরপল লাগবে প্রায় 80.54 বর্গ মিটার |